Trade
International demand
Final demand, intermediate demand, and capital good demand for good \(i\) are aggregated to form total demand \(DEMTOT_{i,s,t}\): \[DEMTOT_{i,s,t} = C_{i,s,t} + \sum_j {IC_{i,j,s,t}} + KG_{i,s,t}.\]
(Standard) Armington assumption
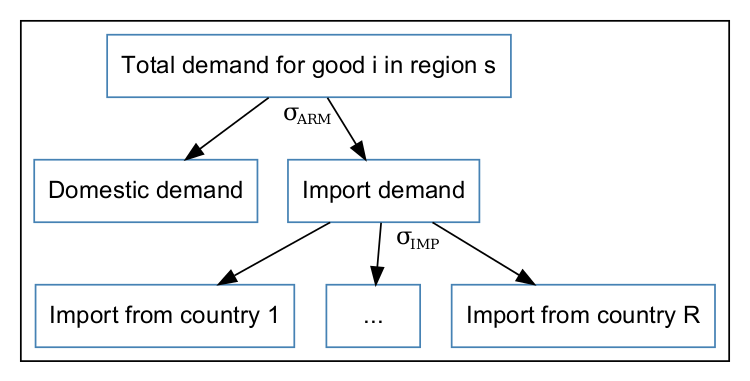
By default, the regional demand in MIRAGE-e uses a standard Armington-type specification using CES functions, with a home bias: it is easier to switch between imports of different origins than between domestic production and imports.
The value of elasticity \(\sigma_{IMP}\) is sourced from the GTAP database, while other elasticities will follow the \(\sqrt{2}\) rule: \[\sigma_{\text{lower level}} - 1 = \sqrt{2}\left(\sigma_{\text{higher level}}-1\right) \]
Trade costs
Trade costs are of two different types in MIRAGE-e:
- Purchasing of international transportation services
- Non-tariff measures
International transportation services
See The Transport Sector.
Non-tariff measures
Data
MIRAGE-e only uses information on the trade-restrictiveness of NTMs (no benefit is considered), using ad-valorem equivalents from:
Modelling
Non-tariff measures (NTMs) can either be modeled as:
- an iceberg trade cost
- an export-tax equivalent (rent-generating)
- an import-tax equivalent (rent-generating)
- any split between the three alternatives
By default, without specific knowledge about the best modeling assumptions, NTMs are assumed to be 1/3 iceberg, 1/3 export-tax equivalent, and 1/3 import-tax equivalent.
In every region, the rents created by import-tax equivalent NTMs on imports and export-tax equivalents on exports are allocated to the representative household by a lump-sum transfer.
Implementation through “generalized” costs
From MIRAGE-e version 1.1, trade costs are separated from standard costs, through the use of endogenous “generalized” tariffs (\(GnTariff_{i,r,s,t}\)), export taxes (\(GnTaxEXP_{i,r,s,t}\)) and iceberg trade costs (\(GnTC_{i,r,s,t}\)):
- \(GnTC_{i,r,s,t} = 1 + tCost_{i,r,s,t} + shareNTM^{tCost}_{i,r,s}\left(tax^{SER}_{i,r,s,t} + NTM_{i,r,s,t}\right)\)
- \(GnTariff_{i,r,s,t} = Tariff_{i,r,s,t} + shareNTM^{Tariff}_{i,r,s} NTM_{i,r,s,t}\)
- \(GnTaxEXP_{i,r,s,t} = tax^{EXP}_{i,r,s,t} + tax^{MFA}_{i,r,s,t} + shareNTM^{taxEXP}_{i,r,s} NTM_{i,r,s,t}\)
Any trade policy scenario has, therefore to be implemented directly on \(Tariff_{i,r,s,t}\), \(tCost_{i,r,s,t}\), \(NTM_{i,r,s,t}\), \(tax_{i,r,s,t}^{SER}\) and \(tax_{i,r,s,t}^{EXP}\)